Lie Group and Lie Algebras 2
Exponential and Logarithmic Mapping
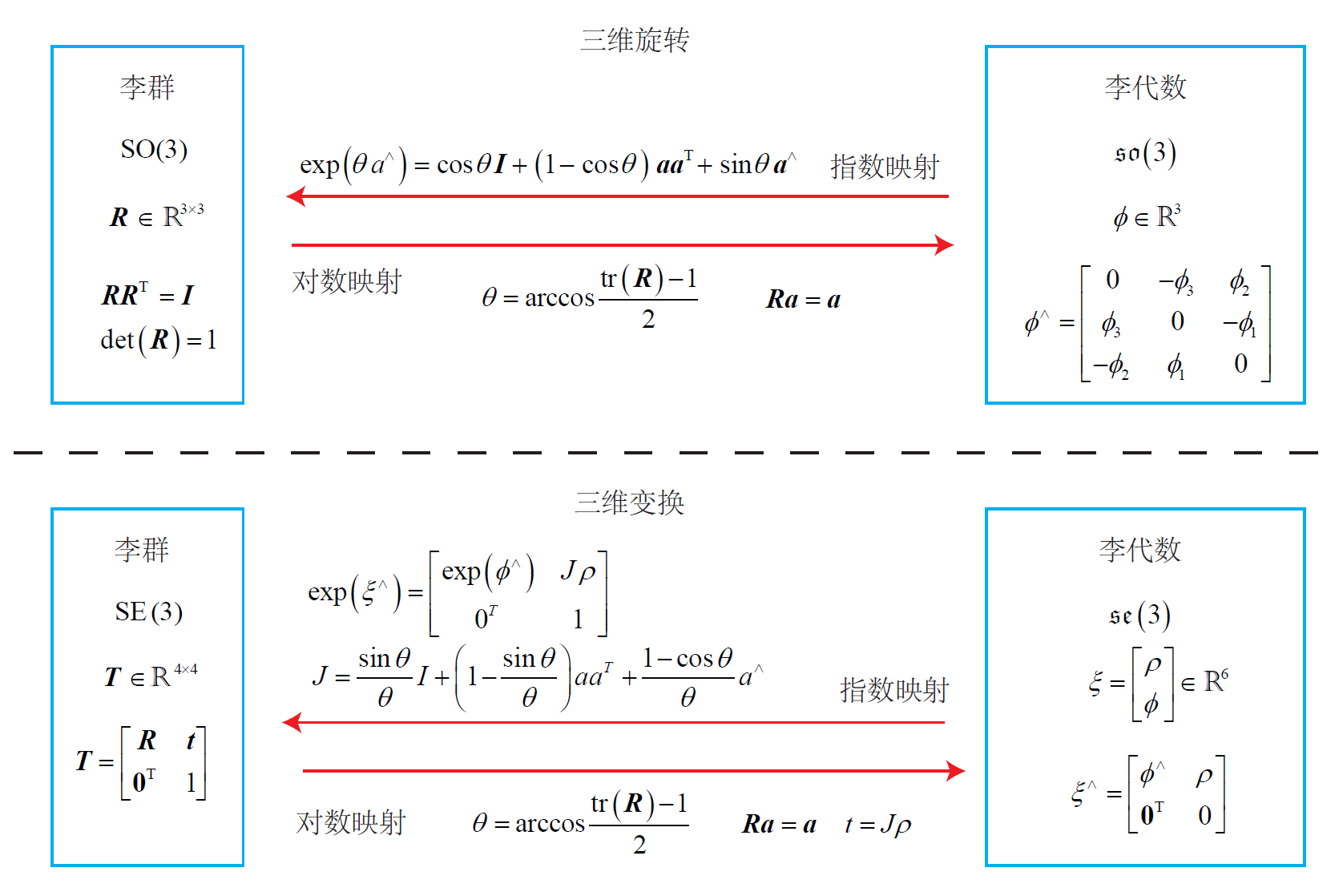
SO(3) Exponential Mapping
考虑如何计算 $exp(\phi^{\wedge})$,它是一个矩阵的指数,因此称之为指数映射。
任意矩阵的指数都可以泰勒展开,但只有在收敛的时候才有结果,其结果仍为矩阵
\begin{equation} \exp(\mathbf{A})=\sum_{n=0}^\infty\frac{1}{n!}\mathbf{A}^n. \end{equation}同样地,对 $\mathfrak{so}(3)$ 中任意元素 $\phi$,可按此方式定义它的指数映射:
\begin{equation} \exp(\phi^{\wedge})=\sum_{n=0}^\infty\frac{1}{n!}(\phi^{\wedge})^n. \end{equation}但该定义涉及矩阵的无穷次幂,难以计算。
由于 $\phi$ 是三维向量,定义其模长和方向分别为 $\theta$ 和 $\boldsymbol{a}$,则 $\phi=\theta \boldsymbol{a}$,这里规定方向向量是单位向量,则 $\parallel \boldsymbol{a}\parallel=1$
对于 $\boldsymbol{a}^{\wedge}$,有以下性质:
\begin{equation} \boldsymbol{a}^\wedge = \left[ \begin{array}{ccc} 0 & -a_3 & a_2 \\ a_3 & 0 & -a_1 \\ -a_2 & a_1 & 0 \\ \end{array} \right] \end{equation} \begin{equation} \boldsymbol{a}^{\wedge}\boldsymbol{a}^{\wedge}=\left[\begin{array}{ccc}-a_2^2-a_3^2&a_1a_2&a_1a_3\\a_1a_2&-a_1^2-a_3^2&a_2a_3\\\\a_1a_3&a_2a_3&-a_1^2-a_2^2\end{array}\right]=\boldsymbol{a}\boldsymbol{a}^{\mathrm{T}}-I \end{equation} \begin{equation} \boldsymbol{a}^{\wedge}\boldsymbol{a}^{\wedge}\boldsymbol{a}^{\wedge}=\boldsymbol{a}^{\wedge}(\boldsymbol{a}\boldsymbol{a}^{\mathrm{T}}-I)=-\boldsymbol{a}^{\wedge} \end{equation}指数映射写成
\begin{aligned} \exp\left(\phi^{\wedge}\right)& =\exp{(\theta \boldsymbol{a}^{\wedge})}=\sum_{n=0}^{\infty}\frac{1}{n!}{(\theta \boldsymbol{a}^{\wedge})}^{n} \\ &=I+\theta \boldsymbol{a}^{\wedge}+\frac1{2!}\theta^{2}\boldsymbol{a}^{\wedge}\boldsymbol{a}^{\wedge}+\frac1{3!}\theta^{3}\boldsymbol{a}^{\wedge}\boldsymbol{a}^{\wedge}\boldsymbol{a}^{\wedge}+\frac1{4!}\theta^{4}\left(\boldsymbol{a}^{\wedge}\right)^{4}+... \\ &=\boldsymbol{a}\boldsymbol{a}^{\mathrm{T}}-\boldsymbol{a}^{\wedge}\boldsymbol{a}^{\wedge}+\theta \boldsymbol{a}^{\wedge}+\frac{1}{2!}\theta^{2}\boldsymbol{a}^{\wedge}\boldsymbol{a}^{\wedge}-\frac{1}{3!}\theta^{3}\boldsymbol{a}^{\wedge}-\frac{1}{4!}\theta^{4}\big(\boldsymbol{a}^{\wedge}\big)^{2}+... \\ &=\boldsymbol{a}\boldsymbol{a}^{\mathrm{T}}+\underbrace{\left(\theta-\frac{1}{3!}\theta^3+\frac{1}{5!}\theta^5-...\right)}_{\sin\theta}\boldsymbol{a}^{\wedge}-\underbrace{\left(1-\frac{1}{2!}\theta^2+\frac{1}{4!}\theta^4-...\right)}_{\cos\theta}\boldsymbol{a}^{\wedge}\boldsymbol{a}^{\wedge} \\ &=\boldsymbol{a}^{\wedge}\boldsymbol{a}^{\wedge}+I+\sin\theta \boldsymbol{a}^{\wedge}-\cos\theta \boldsymbol{a}^{\wedge}\boldsymbol{a}^{\wedge} \\ &=(1-\cos\theta)\boldsymbol{a}^\wedge\boldsymbol{a}^\wedge+\boldsymbol{I}+\sin\theta\boldsymbol{a}^\wedge \\ &=\cos\theta\boldsymbol{I}+(1-\cos\theta)\boldsymbol{a}\boldsymbol{a}^{\mathrm{T}}+\sin\theta \boldsymbol{a}^{\wedge}. \end{aligned}最终的结果为
\begin{equation} \exp(\theta \boldsymbol{a}^{\wedge})=\cos \theta \boldsymbol{I} + (1-\cos \theta)\boldsymbol{a} \boldsymbol{a}^{\mathrm{T}}+\sin \theta \boldsymbol{a}^{\wedge} \end{equation}该公式与罗德里格斯公式形式完全相同。这说明 $\mathfrak{so}(3)$ 是由所谓 旋转向量 组成的空间,而 指数映射即罗德里格斯公式 。
通过它们可以把 $\mathfrak{so}(3)$ 中任意一个向量对应到位于 SO(3)中的旋转矩阵,反之,如果定义对数映射,也能把 SO(3)中的元素对应到 $\mathfrak{so}(3)$ 中
\begin{equation} \phi = \ln (\boldsymbol{R})^{\vee}=\left(\sum_{n=0}^{\infty} \frac{(-1)^n}{n+1}(\boldsymbol{R}-\boldsymbol{I})^{n+1} \right)^{\vee} \end{equation}和指数映射一样,可以使用旋转矩阵计算对应的李代数,利用下式
\begin{equation} \theta=\arccos(\frac{\operatorname{tr}(R)-1}{2}) \end{equation}根据迹的性质分别求解转角和转轴。
指数映射是满射,但不是单射,即每个 SO(3)中的元素都能找到 $\mathfrak{so}(3)$ 对应,但是可能存在多个 $\mathfrak{so}(3)$ 元素对应同一个 SO(3)。
但是如果把旋转角度固定在 $\pm \pi$ 之间,那么李群和李代数是一一对应的。
SE(3)
SE(3)对应的李代数 $\mathfrak{se}(3)$ 的指数映射形式如下:
\begin{equation} \begin{aligned} \exp\left(\xi^{\wedge}\right)& =\left[\begin{array}{cc}{\sum\limits_{n=0}^{\infty}\frac{1}{n!}(\phi^{\wedge})^{n}}&{\sum\limits_{n=0}^{\infty}\frac{1}{(n+1)!}(\phi^{\wedge})^{n}\rho}\\{0^{\mathrm{T}}}&{1}\\\end{array}\right] \\ &\stackrel{\Delta}{=}\left[\begin{array}{cc}R&J\rho\\0^\mathrm{T}&1\end{array}\right]=T \end{aligned} \end{equation}仿照 $\mathfrak{so}(3)$ 推导,令 $\phi = \theta \boldsymbol{a}$,则
\begin{equation} \begin{aligned} \sum_{n=0}^{\infty}\frac{1}{(n+1)!}(\phi^{\wedge})^{n} &= I+\frac{1}{2!}\theta a^{\wedge}+\frac{1}{3!}\theta^{2}(a^{\wedge})^{2}+\frac{1}{4!}\theta^{3}(a^{\wedge})^{3}+\frac{1}{5!}\theta^{4}(a^{\wedge})^{4}\cdots \\ &=\frac{1}{\theta}\left(\frac{1}{2!}\theta^{2}-\frac{1}{4!}\theta^{4}+\cdots\right)(a^{\wedge})+\frac{1}{\theta}\left(\frac{1}{3!}\theta^{3}-\frac{1}{5}\theta^{5}+\cdots\right)\left(a^{\wedge}\right)^{2}+I \\ &=\frac{1}{\theta}\left(1-\cos\theta\right)(a^{\wedge})+\frac{\theta-\sin\theta}{\theta}\left(aa^{T}-I\right)+I \\ &=\frac{\sin\theta}\theta I+\left(1-\frac{\sin\theta}\theta\right)aa^{T}+\frac{1-\cos\theta}\theta a^{\wedge}\stackrel{\Delta}{=}J. \end{aligned} \end{equation}可以看到,$\boldsymbol{R}$ 是 SO(3)中的元素,与 $\mathfrak{se}(3)$ 中的旋转部分 $\phi$ 对应,而 $\boldsymbol{J}$ 则满足
\begin{equation} \boldsymbol{J}=\frac{\sin\theta}\theta I+\left(1-\frac{\sin\theta}\theta\right)aa^{T}+\frac{1-\cos\theta}\theta a^{\wedge} \end{equation}该公式与罗德里格斯公式相似,但不完全一样,平移部分经过指数映射后发生了一次以 $\boldsymbol{J}$ 为系数矩阵的线性变换。
此处也可以类比推导对数映射。
根据变换矩阵 $T$ 可以求得 $\mathfrak{so}(3)$ 的对应向量:
- 左上角的 $R$ 计算旋转向量
- 右上角的 $t$ 满足 $t=\boldsymbol{J} \boldsymbol{\rho}$
Differentiation
以上讨论 SO(3)和 SE(3)的关系(即李群与李代数的关系),但在 SO(3)完成两个矩阵乘法的时候,李代数 $\mathfrak{so}(3)$ 上怎样改变?
BCH Equation
矩阵的指数函数不满足
\begin{equation} \exp\left(\phi_1^{\wedge}\right)\exp\left(\phi_2^{\wedge}\right) \ne \exp\left((\phi_1+\phi_2)^{\wedge}\right) \end{equation}或者说不满足
\begin{equation} \ln\left(\exp\left(A\right)\exp\left(B\right)\right)\ne A+B \end{equation}两个李代数指数映射乘积的完整形式为 Baker-Campbell-Hausdorff 公式给出,其展开式的前几项为:
\begin{equation} \begin{aligned}\ln\left(\exp\left(A\right)\exp\left(B\right)\right)&=A+B+\frac{1}{2}\left[A,B\right]+\frac{1}{12}\left[A,\left[A,B\right]\right]-\frac{1}{12}\left[B,\left[A,B\right]\right]+\cdots\end{aligned} \end{equation}BCH 公式指出,当处理两个矩阵的指数之积时,它们会产生李括号余项。
考虑 SO(3)上的李代数 $\ln(\exp(\phi_1^{\wedge})\exp(\phi_2^{\wedge}))^{\vee}$,当 $\phi_1$ 或 $\phi_2$ 为小量时,小量二次以上的项都可以被忽略掉。此时
\begin{equation} \left.\ln\left(\exp\left(\phi_1^{\wedge}\right)\exp\left(\phi_2^{\wedge}\right)\right)^{\vee}\approx\left\{\begin{array}{ll}J_{l}(\phi_2)^{-1}\phi_1+\phi_2&\text{当}\phi_1\text{为小量},\\J_{r}(\phi_1)^{-1}\phi_2+\phi_1&\text{当}\phi_2\text{为小量}.\end{array}\right.\right. \end{equation}第一个近似说明当对一个旋转矩阵 $R_2$ (其李代数为 $\phi_2$ ) 左乘一个微小旋转矩阵 $R_1$ (其李代数为 $\phi_1$)时,可以近似地看作,在原有的李代数 $\phi_{2}$ 上加上了一项 $J_l(\phi_2)^{-1}\phi_1$
第二个近似说明当对一个旋转矩阵 $R_1$ (其李代数为 $\phi_1$ ) 右乘一个微小旋转矩阵 $R_2$ (其李代数为 $\phi_2$)时,可以近似地看作,在原有的李代数 $\phi_{1}$ 上加上了一项 $J_l(\phi_1)^{-1}\phi_2$
于是,李代数在 BCH 近似下,分成了左乘近似和右乘近似两种,在使用时须注意使用的是左乘模型还是右乘模型。
左乘 BCH 近似雅可比 $\boldsymbol{J}_l$
\begin{equation} J_{l}=J =\frac{\sin\theta}\theta I+\left(1-\frac{\sin\theta}\theta\right)aa^{\mathrm{T}}+\frac{1-\cos\theta}\theta a^{\wedge} \end{equation}其逆为
\begin{equation} J_{l}^{-1} =\frac{\theta}{2}\cot\frac{\theta}{2}I+\left(1-\frac{\theta}{2}\cot\frac{\theta}{2}\right)aa^{\mathrm{T}}-\frac{\theta}{2}a^{\wedge} \end{equation}而右乘雅可比仅需对自变量取负号
\begin{equation} J_r(\phi)=J_l(-\phi) \end{equation}BCH Meaning
BCH 近似的意义:
假定对某个旋转 $R$ ,对应的李代数为 $\phi$ ,给它左乘一个微小旋转,记作 $\Delta R$, 对应的李代数为 $\Delta\phi$。
在李群上,得到的结果是$\Delta R\cdot R$ ,而在李代数上,根据 BCH 近似,为 $J_l^{-1}(\phi)\Delta\phi+\phi$。
合并起来,简写成
\begin{equation} \exp\left(\Delta\phi^{\wedge}\right)\exp\left(\phi^{\wedge}\right)=\exp\left(\left(\phi+J_{l}^{-1}\left(\phi\right)\Delta\phi\right)^{\wedge}\right) \end{equation}反之,如果需要在李代数上进行加法,让一个 $\phi$ 加上 $\Delta\phi$,那么可以近似为李群上带左右雅可比的乘法
\begin{equation} \exp\left(\left(\phi+\Delta\phi\right)^{\wedge}\right)=\exp\left(\left(J_{l}\Delta\phi\right)^{\wedge}\right)\exp\left(\phi^{\wedge}\right)=\exp\left(\phi^{\wedge}\right)\exp\left(\left(J_{r}\Delta\phi\right)^{\wedge}\right) \end{equation}对于 SE(3),也有类似的 BCH 近似
\begin{equation} \begin{aligned}\exp\left(\Delta\xi^{\wedge}\right)\exp\left(\xi^{\wedge}\right)&\approx\exp\left(\left(\mathcal{J}_{l}^{-1}\Delta\xi+\xi\right)^{\wedge}\right),\\\\\exp\left(\xi^{\wedge}\right)\exp\left(\Delta\xi^{\wedge}\right)&\approx\exp\left(\left(\mathcal{J}_{r}^{-1}\Delta\xi+\xi\right)^{\wedge}\right).\end{aligned} \end{equation}SO(3) Lie Algebras Differentiation Basic
讨论一个带有李代数的函数,如何关于该李代数求导。
在 SLAM 中要估计一个相机的位置和姿态,该位姿是由 SO(3) 上的旋转矩阵或 SE(3) 上的变 换矩阵描述。
设某个时刻位姿为 $T$ ,它观察到一个世界坐标位于 $p$ 的点,产生了观测数据 $z$ 。那么,由坐标变换关系知:
\begin{equation} z=Tp+w \end{equation}其中 $w$ 为随机噪声,$z$ 不能精确的满足 $z=Tp$ 的关系,计算观测与实际的误差
\begin{equation} e=z-Tp \end{equation}设总共有 $N$ 个路标和观测,则寻找最优的 $T$ 使得整体误差最小化
\begin{equation} \min_TJ(T)=\sum_{i=1}^N\left\|z_i-Tp_i\right\|_2^2 \end{equation}求解该优化问题,需要计算目标函数 $J$ 关于变换矩阵 $T$ 的导数。
- 需要构建与位姿有关的函数,然后讨论该函数关于位姿的导数,以调整当前
的估计值。
- SO(3); SE(3) 上并没有良好定义的加法,它们只是群。如果把 $T$ 当成一个普通矩阵来处理优化,那就必须对它加以约束。
- 从李代数角度来说,由于李代数由向量组成,具有良好的加法运算。
因此,使用李代数解决求导问题的思路:
- 用李代数表示姿态,然后根据李代数加法来对李代数求导。
- 对李群左乘或右乘微小扰动,然后对该扰动求导,分为左扰动和右扰动。
SO(3) Lie Algebras Differentiation Process
考虑 SO(3) 上,假设我们对一个空间点 $p$ 进行了旋转,得到了 $Rp$。
现在,要计算旋转之后点的坐标相对于旋转的导数,记为 $\frac{\partial\left(Rp\right)}{\partial R}$
由于 SO(3) 没有加法,所以该导数无法按照导数的定义进行计算。根据旋转矩阵 $R$ 对应的李代数 $\phi$ 转而计算 $\frac{\partial\left(\exp\left(\phi^{\wedge}\right)p\right)}{\partial\phi}$
需要注意:
- 严格说来,在矩阵微分中,只能求行向量关于列向量的导数,所得结果是一个矩阵
- 此处写成列向量对列向量的导数,可以认为是先对分子进行转置,再对最后结果进行转置
- 这样式子变得简洁,不然就不得不给每一行的分子加一个转置符号
在以上这种意义下,可以认为 $\frac{d(Ax)}{dx} = A$。
按导数定义有
\begin{equation} \begin{aligned} \frac{\partial\left(\exp\left(\phi^{\wedge}\right)p\right)}{\partial\phi}& =\lim_{\delta\phi\to\mathbf{0}}\frac{\exp\left(\left(\phi+\delta\phi\right)^{\wedge}\right)p-\exp\left(\phi^{\wedge}\right)p}{\delta\phi} \\ &=\lim_{\delta\phi\to\mathbf{0}}\frac{\exp\left(\left(J_l\delta\phi\right)^{\wedge}\right)\exp\left(\phi^{\wedge}\right)p-\exp\left(\phi^{\wedge}\right)p}{\delta\phi} \\ &=\lim_{\delta\phi\to\mathbf{0}}\frac{\left(I+\left(J_l\delta\phi\right)^{\wedge}\right)\exp\left(\phi^{\wedge}\right)p-\exp\left(\phi^{\wedge}\right)p}{\delta\phi} \\ &=\lim_{\delta\boldsymbol{\phi}\to\boldsymbol{0}}\frac{(J_l\delta\phi)^{\wedge}\exp\left(\phi^{\wedge}\right)p}{\delta\phi} \\ &=\lim_{\delta\phi\to\mathbf{0}}\frac{-(\exp\left(\phi^{\wedge}\right)p)^{\wedge}J_{l}\delta\phi}{\delta\phi}=-(Rp)^{\wedge}J_{l}. \end{aligned} \end{equation}其中,第 2 行的近似为 BCH 线性近似,第 3 行为泰勒展开舍去高阶项后的近似(但由于取了极限,可以写等号),第 4 行至第 5 行将反对称符号看作叉积,交换之后变号。
旋转后的点相对于李代数的导数为
\begin{equation} \frac{\partial\left(Rp\right)}{\partial\phi}=\left(-Rp\right)^{\wedge}J_{l} \end{equation}然而这里仍然含有形式复杂的 $\boldsymbol{J}_l$
Pertubation Model
SO(3) Pertubation Model
另一种求导方式是对 R 进行一次扰动 $\delta R$,看结果相对于扰动的变化率。这个扰动可以乘在左边也可以乘在右边,最后结果会有一点儿微小的差异
以左扰动为例。设左扰动ΔR 对应的李代数为 $\phi$,对 $\phi$ 求导,即
\begin{equation} \begin{aligned} \frac{\partial\left(Rp\right)}{\partial\varphi}& =\lim_{\varphi\to0}\frac{\exp\left(\varphi^{\wedge}\right)\exp\left(\phi^{\wedge}\right)p-\exp\left(\phi^{\wedge}\right)p}{\varphi} \\ &=\lim_{\varphi\to0}\frac{\left(I+\varphi^{\wedge}\right)\exp\left(\phi^{\wedge}\right)p-\exp\left(\phi^{\wedge}\right)p}\varphi \\ &=\lim_{\varphi\to0}\frac{\varphi^{\wedge}Rp}\varphi=\lim_{\varphi\to0}\frac{-(Rp)^{\wedge}\varphi}\varphi=-(Rp)^{\wedge}. \end{aligned} \end{equation}这里相比于直接对李代数求导,省略了雅可比 $\boldsymbol{J}_l$ 的计算。
SE(3) Pertubation Model
最后,讨论 SE(3)上的扰动模型
假设某空间点 $p$ 经过一次变换 $T$ (对应李代数为 $\xi$ ),得到 $Tp^\mathrm{o}$,给 $T$ 左乘一个扰动 $\Delta T=\exp\left(\delta\xi^\wedge\right)$,设扰动项的李代数为 $\delta\xi=[\delta\rho,\delta\phi]^{\mathrm{T}}$,则
\begin{equation} \begin{aligned} \frac{\partial\left(Tp\right)}{\partial\delta\xi}& =\lim_{\delta\boldsymbol{\xi}\to\boldsymbol{0}}\frac{\exp\left(\delta\xi^{\wedge}\right)\exp\left(\xi^{\wedge}\right)p-\exp\left(\xi^{\wedge}\right)p}{\delta\xi} \\ &=\lim_{\delta\boldsymbol{\xi}\to\boldsymbol{0}}\frac{\left(I+\delta\xi^{\wedge}\right)\exp\left(\xi^{\wedge}\right)p-\exp\left(\xi^{\wedge}\right)p}{\delta\xi} \\ &=\lim_{\delta\boldsymbol{\xi}\to\boldsymbol{0}}\frac{\delta\xi^{\wedge}\exp\left(\xi^{\wedge}\right)p}{\delta\xi} \\ &=\lim_{\delta\boldsymbol{\xi}\to\boldsymbol{0}}\frac{\left[\begin{array}{cc}\delta\phi^\wedge&\delta\rho\\0^\mathrm{T}&0\end{array}\right]\left[\begin{array}{c}Rp+t\\1\end{array}\right]}{\delta\boldsymbol{\xi}} \\ &=\lim_{\delta\boldsymbol{\xi}\to\boldsymbol{0}}\frac{\left[\begin{array}{c}\delta\phi^{\wedge}\left(Rp+t\right)+\delta\rho\\0^\mathrm{T}\end{array}\right]}{[\delta\rho,\delta\phi]^\mathrm{T}}=\left[\begin{array}{cc}I&-(Rp+t)^{\wedge}\\0^\mathrm{T}&0^\mathrm{T}\end{array}\right]\triangleq(Tp)^\odot \end{aligned} \end{equation}定义最后的结果为一个算符${\odot}$,它把一个齐次坐标的空间点变换成一个 $4 \times 6$ 的矩阵
特别需要注明的是矩阵求导方面的顺序,假设 $a,b,x,y$ 都是列向量,那么存在
\begin{equation} \frac{\mathrm{d}\begin{bmatrix}a\\\\b\end{bmatrix}}{\mathrm{d}\begin{bmatrix}x\\\\y\end{bmatrix}}=\left(\frac{\mathrm{d}[a,b]^\mathrm{T}}{\mathrm{d}\begin{bmatrix}x\\\\y\end{bmatrix}}\right)^\mathrm{T}=\begin{bmatrix}\frac{\mathrm{d}a}{\mathrm{d}x}&\frac{\mathrm{d}b}{\mathrm{d}x}\\\frac{\mathrm{d}a}{\mathrm{d}y}&\frac{\mathrm{d}b}{\mathrm{d}y}\end{bmatrix}^\mathrm{T}=\begin{bmatrix}\frac{\mathrm{d}a}{\mathrm{d}x}&\frac{\mathrm{d}a}{\mathrm{d}y}\\\frac{\mathrm{d}b}{\mathrm{d}x}&\frac{\mathrm{d}b}{\mathrm{d}y}\end{bmatrix} \end{equation}